Contenu
En géométrie, un octogone est un polygone à huit côtés. Un octogone régulier a huit côtés égaux et angles égaux. L'octogone régulier est généralement reconnu par les panneaux d'arrêt. Un octaèdre est un polyèdre à huit faces. Un octaèdre régulier a huit triangles avec des arêtes d'égale longueur. Il s’agit bien de deux pyramides carrées se rejoignant à leurs bases.
Formule Zone Octogone
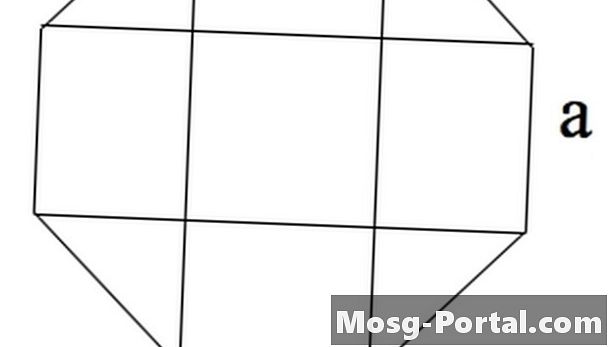
La formule pour l'aire d'un octogone régulier dont les côtés de longueur "a" est 2 (1 + sqrt (2)) a ^ 2, où "sqrt" indique la racine carrée.
Dérivation
Un octogone peut être vu comme 4 rectangles, un carré au centre et quatre triangles isocèles dans les coins.
Le carré est de surface a ^ 2.
Les triangles ont les côtés a, / sqrt (2) et a / sqrt (2), du théorème de Pythagore. Par conséquent, chacun a une superficie de ^ 2/4.
Les rectangles ont une aire a * a / sqrt (2).
La somme de ces 9 zones est 2a ^ 2 (1 + sqrt (2)).
Formule Volume Octaèdre
La formule pour le volume d'un octaèdre régulier de côtés "a" est un ^ 3 * sqrt (2) / 3.
Dérivation
L'aire d'une pyramide à quatre côtés est l'aire base * hauteur / 3. L'aire d'un octogone régulier est donc 2 * base * hauteur / 3.
Base = a ^ 2 trivialement.
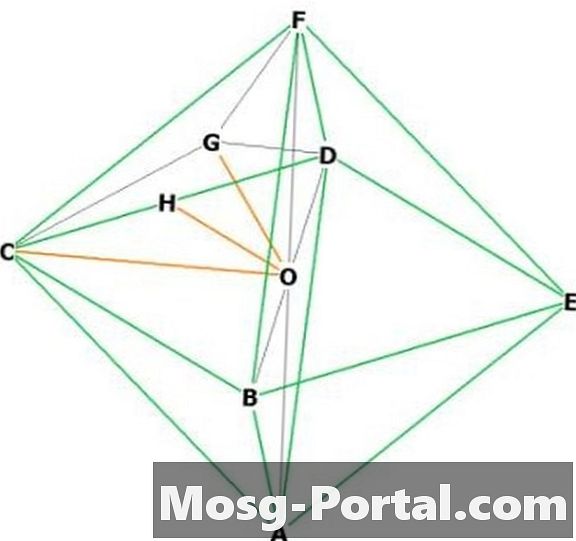
Choisissez deux sommets adjacents, dites "F" et "C." "O" est au centre. FOC est un triangle rectangle isocèle dont la base est "a", donc OC et OF ont pour longueur a / sqrt (2) selon le théorème de Pythagore. Donc hauteur = a / sqrt (2).
Ainsi, le volume d'un octaèdre régulier est 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Surface
La surface des octaèdres réguliers est l’aire d’un triangle équilatéral de côté "a" fois 8 faces.
Pour utiliser le théorème de Pythagore, tracez une ligne du sommet à la base. Cela crée deux triangles rectangles, avec l'hypoténuse de longueur "a" et une longueur de côté "a / 2". Par conséquent, le troisième côté doit être sqrt = sqrt (3) a / 2. L'aire d'un triangle équilatéral est donc égale à la hauteur * base / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Avec 8 côtés, la surface d’un octaèdre régulier est de 2 * sqrt (3) * a ^ 2.