Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur. La surface d'un polygone à deux dimensions tel qu'un triangle est la surface totale contenue par les côtés du polygone. Les trois angles d'un triangle équilatéral sont également égaux en géométrie euclidienne. Étant donné que la mesure totale des angles d'un triangle euclidien est de 180 degrés, cela signifie que les angles d'un triangle équilatéral mesurent tous 60 degrés. L'aire d'un triangle équilatéral peut être calculée lorsque la longueur de l'un de ses côtés est connue.

Détermine l'aire d'un triangle lorsque la base et la hauteur sont connues. Prenez deux triangles identiques avec la base s et la hauteur h. On peut toujours former un parallélogramme de base s et de hauteur h avec ces deux triangles. Puisque l'aire d'un parallélogramme est s x h, l'aire A d'un triangle est donc ½ s x h.

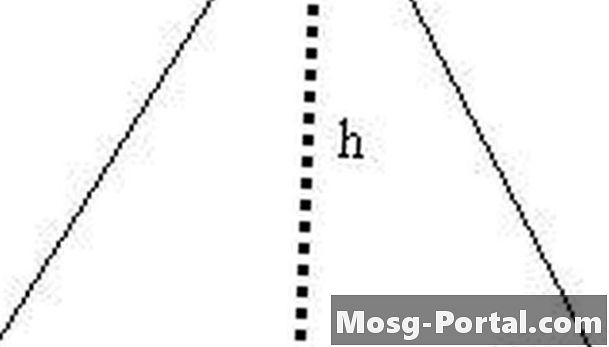
Formez le triangle équilatéral en deux triangles rectangles avec le segment de droite h. L'hypoténuse de l'un de ces triangles rectangles de longueur s, l'une des jambes a la longueur h et l'autre jambe, la longueur s / 2.
Exprimer h en termes de s. En utilisant le triangle rectangle formé à l’étape 2, nous savons que s ^ 2 = (s / 2) ^ 2 + h ^ 2 par la formule de Pythagore. Donc h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, et nous avons maintenant h = (3 ^ 1/2) s / 2.
Remplacez la valeur de h obtenue à l'étape 3 par la formule d'une zone de triangles obtenue à l'étape 1. Comme A = ½ sxh et h = (3 ^ 1/2) s / 2, nous avons maintenant A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Utilisez la formule de l'aire d'un triangle équilatéral obtenue à l'étape 4 pour trouver l'aire d'un triangle équilatéral de côtés de longueur 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).