
L'autocorrélation est une méthode statistique utilisée pour l'analyse de séries chronologiques. Le but est de mesurer la corrélation de deux valeurs dans le même ensemble de données à des intervalles de temps différents. Bien que les données temporelles ne soient pas utilisées pour calculer l'autocorrélation, vos incréments de temps doivent être égaux pour obtenir des résultats significatifs. Le coefficient d'autocorrélation a deux objectifs. Il peut détecter le caractère non aléatoire dans un ensemble de données. Si les valeurs de l'ensemble de données ne sont pas aléatoires, une autocorrélation peut aider l'analyste à choisir un modèle de série chronologique approprié.
Calculez la moyenne ou la moyenne des données que vous analysez. La moyenne est la somme de toutes les valeurs de données divisée par le nombre de valeurs de données (n).
Déterminez un décalage (k) pour votre calcul. La valeur de décalage est un entier indiquant le nombre de pas de temps séparant une valeur d'une autre. Par exemple, le décalage entre (y1, t1) et (y6, t6) est de cinq, car il y a 6 - 1 = 5 intervalles de temps entre les deux valeurs. Lorsque vous testez le caractère aléatoire, vous ne calculerez généralement qu'un seul coefficient d'autocorrélation en utilisant le décalage k = 1, bien que d'autres valeurs de décalage fonctionnent également. Lorsque vous déterminez un modèle de série chronologique approprié, vous devez calculer une série de valeurs d'autocorrélation, en utilisant une valeur de décalage différente pour chacune.
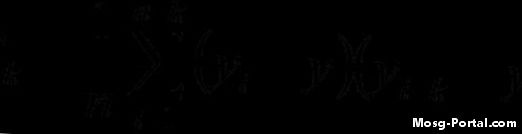
Calculez la fonction d'autovariance à l'aide de la formule donnée. Par exemple, si vous calculiez la troisième itération (i = 3) en utilisant un décalage k = 7, le calcul de cette itération ressemblerait à ceci: (y3 - barre y) (y10 - barre y) Parcourez tout les valeurs de "i" puis prenez la somme et divisez-la par le nombre de valeurs de l'ensemble de données.
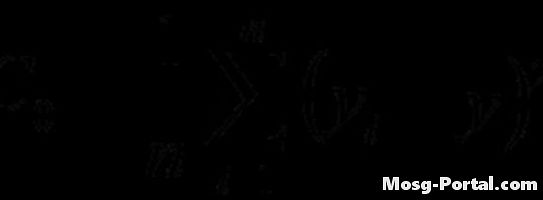
Calculez la fonction de variance en utilisant la formule donnée. Le calcul est similaire à celui de la fonction d’autocovariance, mais le décalage n’est pas utilisé.

Divisez la fonction d'autovariance par la fonction de variance pour obtenir le coefficient d'autocorrélation. Vous pouvez contourner cette étape en divisant les formules des deux fonctions, comme indiqué, mais vous aurez souvent besoin de l'autovariance et de la variance à d'autres fins. Il est donc pratique de les calculer individuellement.