Contenu
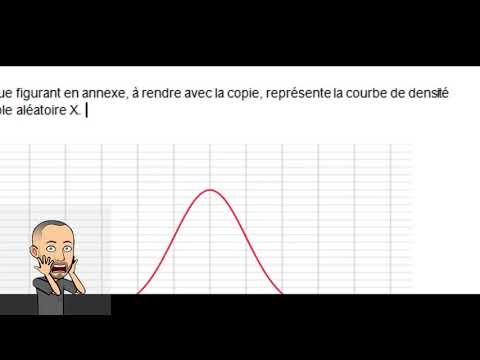
Une courbe en cloche donne à une personne qui étudie un fait un exemple de distribution normale d'observations. La courbe s'appelle également la courbe gaussienne d'après le mathématicien allemand Carl Friedrich Gauss, qui a découvert de nombreuses propriétés des courbes. Une courbe représente approximativement la plage et compte pour de nombreuses observations réelles de faits existant dans la nature et dans la société civile, tels que le poids et les performances éducatives.
Choisissez le fait pour lequel vous voulez une distribution de probabilité normale. Considérez comment l’exemple des événements normaux vous aidera à tirer une conclusion. Résolvez les questions décisives concernant votre fait. Une distribution de poids normale est-elle utile pour étudier les poids dans une population de patients en médecine? Ou la population est-elle trop inhabituelle ou anormale pour utiliser une courbe normale?
Faites un ensemble de données pour vos observations que vous prévoyez de tracer. Pour chaque sujet, notez le fait sous forme de valeur numérique. Attribuez un numéro à chaque sujet et étiquetez l’observation "x numéro de sous-sujet. " Disposez les valeurs "x " du plus bas au plus élevé. Attribuez à chaque sujet un second numéro, le numéro de commande de la valeur d'observation, et étiquetez ces observations "x numéro de sous-commande ".
Attribuez la plage de numéros pour les valeurs numériques, en utilisant l'observation la plus basse à l'observation la plus élevée.
Utilisez la formule de la courbe en cloche pour calculer la valeur de l’axe des y pour chaque valeur de l’axe des x. La formule de la courbe en cloche est y = (e ^ (? - x? ^ 2/2)) /? 2 ?. Y est le nombre d'observations pour une valeur x. Le x est une valeur observée. Utilisez le numéro de sous-commande x pour l'ordre de calcul et l'ordre de la liste. Créez une table de valeurs x et des valeurs y correspondantes.
Graphique de la courbe de cloche pour votre fait. En utilisant du papier graphique, organisez un graphique avec un axe x et un axe y. Tracez la plage d'axes pour commencer à la valeur la plus basse et se terminer à la valeur la plus élevée. Commencez l'axe des ordonnées à 0 pour aucune observation et terminez par le plus grand nombre d'observations possibles pour toute valeur x. Le plus grand potentiel d'observations est le plus grand nombre que vous croyez pouvoir trouver pour votre fait; par exemple, le plus grand nombre de patients de sexe masculin pesant 180 livres.
Lorsque vous souhaitez comparer vos faits observés à une distribution normale, affichez un graphique de vos observations et la courbe normale que vous avez représentée. Comparez la manière dont les observations réelles se situent dans les zones d’un écart-type de la moyenne. Lorsque vous disposez d'un bon ensemble de données pour une population normale, 90% de vos observations se situent à moins de 1,65 écart-type, à gauche et à droite de la moyenne de la courbe normale. Les différences de la courbe normale vous indiquent que votre population est supérieure à la moyenne, lorsque la moyenne des observations réelles est à droite, ou inférieure à la moyenne, lorsque votre moyenne observée est à gauche.