Une ellipse peut être définie en géométrie plane comme un ensemble de points tel que la somme de leurs distances à deux points (foyers) soit constante. La figure obtenue peut également être décrite de manière non mathématique comme un ovale ou un "cercle aplati". Les ellipses ont de nombreuses applications en physique et sont particulièrement utiles pour décrire les orbites planétaires. L'excentricité est l'une des caractéristiques de l'ellipse et est une mesure de la façon dont l'ellipse est circulaire.
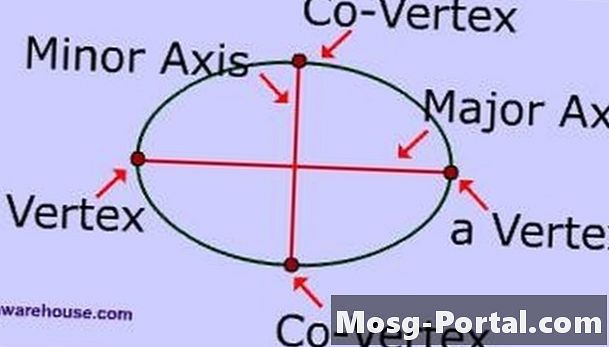
Examinez les parties d'une ellipse. L'axe principal est le segment de droite le plus long qui coupe le centre de l'ellipse et dont les extrémités se trouvent sur l'ellipse. L'axe mineur est le segment de droite le plus court qui coupe le centre de l'ellipse et dont les extrémités se trouvent sur l'ellipse. Le demi-axe majeur correspond à la moitié du grand axe et le demi-axe mineur à la moitié du petit axe.
Examiner la formule pour une ellipse. Il existe différentes manières de décrire mathématiquement une ellipse, mais la plus utile pour calculer son excentricité concerne une ellipse est la suivante: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Les constantes a et b sont spécifiques à une ellipse particulière et les variables sont les coordonnées x et y des points situés sur l’ellipse. Cette équation décrit une ellipse dont le centre est l’origine et les axes majeurs et mineurs qui se trouvent sur les origines x et y.
Identifier les longueurs des demi-axes. Dans l'équation x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1, les longueurs des demi-axes sont données par a et b. La valeur la plus grande représente le demi-axe principal et la valeur la plus petite, le demi-axe mineur.
Calculer les positions des foyers. Les foyers sont situés sur le grand axe, un de chaque côté du centre. Étant donné que les axes d'une ellipse se trouvent sur les lignes d'origine, une coordonnée sera 0 pour les deux foyers. L’autre coordonnée pour sera (a ^ 2 - b ^ 2) ^ (1/2) pour un foyer et - (a ^ 2 - b ^ 2) ^ (1/2) pour l’autre foyer où a> b.
Calculez l'excentricité de l'ellipse en tant que rapport de la distance d'un foyer du centre à la longueur du demi-grand axe. L'excentricité e est donc (a ^ 2 - b ^ 2) ^ (1/2) / a. Notez que 0 <= e <1 pour toutes les ellipses. Une excentricité égale à 0 signifie que l'ellipse est un cercle et qu'une ellipse longue et mince a une excentricité proche de 1.