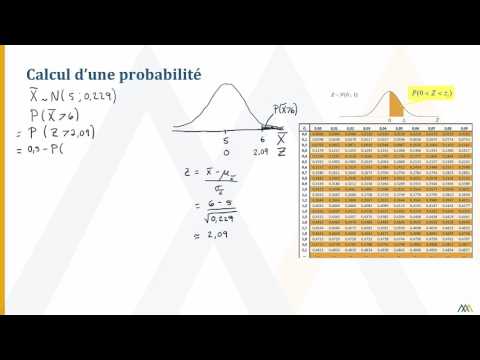
La distribution d'échantillonnage de la moyenne est un concept important en statistique et est utilisée dans plusieurs types d'analyses statistiques. La distribution de la moyenne est déterminée en prenant plusieurs ensembles d'échantillons aléatoires et en calculant la moyenne à partir de chacun. Cette distribution des moyennes ne décrit pas la population elle-même, elle décrit la moyenne de la population. Ainsi, même une distribution de population très asymétrique donne une distribution normale de la moyenne en forme de cloche.
Prenez plusieurs échantillons d'une population de valeurs. Chaque échantillon devrait avoir le même nombre de sujets. Même si chaque échantillon contient des valeurs différentes, elles ressemblent en moyenne à la population sous-jacente.
Calculez la moyenne de chaque échantillon en prenant la somme des valeurs de l'échantillon et en la divisant par le nombre de valeurs de l'échantillon. Par exemple, la moyenne des échantillons 9, 4 et 5 est (9 + 4 + 5) / 3 = 6. Répétez cette procédure pour chacun des échantillons prélevés. Les valeurs résultantes sont votre échantillon de moyennes. Dans cet exemple, l'échantillon de moyenne est 6, 8, 7, 9, 5.
Prenez la moyenne de votre échantillon de moyennes. La moyenne de 6, 8, 7, 9 et 5 est (6 + 8 + 7 + 9 + 5) / 5 = 7.
La distribution de la moyenne a son maximum à la valeur résultante. Cette valeur se rapproche de la vraie valeur théorique de la moyenne de la population. La moyenne de population ne peut jamais être connue car il est pratiquement impossible d'échantillonner chaque membre d'une population.
Calculez l'écart type de la distribution. Soustrayez la moyenne des moyennes d'échantillon de chaque valeur de l'ensemble. Place le résultat. Par exemple, (6 - 7) ^ 2 = 1 et (8 - 6) ^ 2 = 4. Ces valeurs sont appelées écarts carrés. Dans l'exemple, l'ensemble des écarts carrés est 1, 4, 0, 4 et 4.
Additionnez les déviations au carré et divisez par (n - 1), le nombre de valeurs de l'ensemble moins un. Dans l'exemple, il s'agit de (1 + 4 + 0 + 4 + 4) / (5 - 1) = (14/4) = 3,25. Pour trouver l'écart type, prenons la racine carrée de cette valeur, qui est égale à 1,8. C'est l'écart type de la distribution d'échantillonnage.
Indiquez la distribution de la moyenne en incluant sa moyenne et son écart type. Dans l'exemple ci-dessus, la distribution indiquée est (7, 1,8). La distribution d'échantillonnage de la moyenne prend toujours une distribution normale, ou en forme de cloche.