Contenu
- La parabole
- Le mathématicien Menaechmus
- Le nom "Parabole"
- Galileo et Projectile Motion
- Réflecteurs paraboliques
- Ponts suspendus
Les courbes mathématiques telles que la parabole n'ont pas été inventées. Au contraire, ils ont été découverts, analysés et mis à profit. La parabole a une variété de descriptions mathématiques, a une longue et intéressante histoire en mathématiques et en physique, et est utilisée dans de nombreuses applications pratiques de nos jours.
La parabole
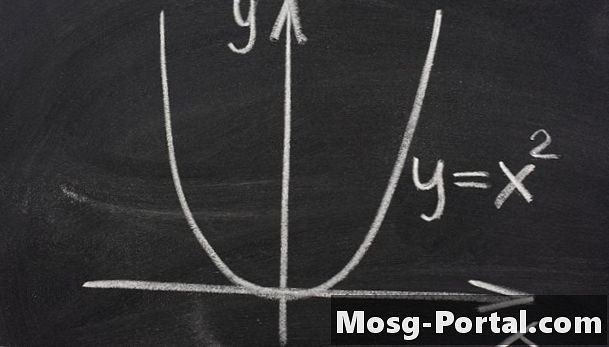
Une parabole est une courbe continue qui ressemble à un bol ouvert dont les côtés continuent de monter à l'infini. Une définition mathématique d'une parabole est l'ensemble des points qui se trouvent tous à la même distance d'un point fixe appelé le foyer et d'une ligne appelée directrice. Une autre définition est que la parabole est une conique particulière. Cela signifie que c'est une courbe que vous voyez si vous coupez à travers un cône. Si vous coupez parallèlement à un côté du cône, vous voyez une parabole. Une parabole est également la courbe définie par l'équation y = ax ^ 2 + bx + c lorsque la courbe est symétrique autour de l'axe des ordonnées. Une équation plus générale existe également pour d'autres situations.
Le mathématicien Menaechmus
Le mathématicien grec Menaechmus (milieu du IVe siècle av. J.-C.) aurait découvert que la parabole était une section conique. On lui attribue également l’utilisation de paraboles pour résoudre le problème de la construction géométrique de la racine cubique de deux. Menaechmus n'a pas été en mesure de résoudre ce problème avec une construction, mais il a montré qu'il est possible de trouver la solution en croisant deux courbes paraboliques.
Le nom "Parabole"
On attribue au mathématicien grec Apollonius de Perga (IIIe au IIe siècle av. J.-C.) le nom de la parabole. "Parabole" vient du mot grec signifiant "application exacte", qui, selon le dictionnaire en ligne d'étymologie, est "parce qu'elle est produite par" l'application "d'une zone donnée à une droite donnée".
Galileo et Projectile Motion
À l’époque de Galilée, on savait que les corps tombaient droit selon la règle des carrés: la distance parcourue était proportionnelle au carré du temps. Cependant, la nature mathématique de la trajectoire générale du mouvement du projectile n’était pas connue. Avec l'avènement des canons, cela devenait un sujet d'importance. En reconnaissant que mouvement horizontal et mouvement vertical sont indépendants, Galileo a montré que les projectiles suivent une trajectoire parabolique. Sa théorie fut finalement validée comme un cas particulier de la loi de gravitation de Newton.
Réflecteurs paraboliques
Un réflecteur parabolique a la capacité de focaliser ou de concentrer l'énergie venant directement vers lui. La télévision par satellite, les radars, les tours de téléphonie mobile et les capteurs sonores utilisent tous la propriété de focalisation des réflecteurs paraboliques.D'énormes radiotélescopes concentrent les signaux faibles de l'espace pour créer des images d'objets distants, et de nombreux énormes sont utilisés de nos jours. Les télescopes à lumière réfléchissante fonctionnent également sur ce principe. Malheureusement, le récit selon lequel Archimède aurait aidé une armée grecque à utiliser des miroirs paraboliques pour mettre le feu aux envahisseurs romains attaquant leur ville de Syracuse en 213 av. J.-C. n'est probablement pas plus qu'une légende. Le processus de mise au point fonctionne également en sens inverse: l’énergie émise vers le miroir par le foyer se reflète dans un faisceau rectiligne très uniforme. Les lampes et les émetteurs, tels que les radars et les micro-ondes, émettent des faisceaux dirigés d'énergie réfléchie par une source au foyer.
Ponts suspendus
Si vous tenez les deux bouts d’une corde, elle s’enfonce dans une courbe appelée caténaire. Certaines personnes confondent cette courbe avec une parabole, mais ce n'en est pas une. Fait intéressant, si vous suspendez des poids à la corde, la courbe change de forme de sorte que les points de suspension reposent sur une parabole et non sur une caténaire. Ainsi, les câbles suspendus des ponts suspendus forment en réalité des paraboles et non des caténaires.