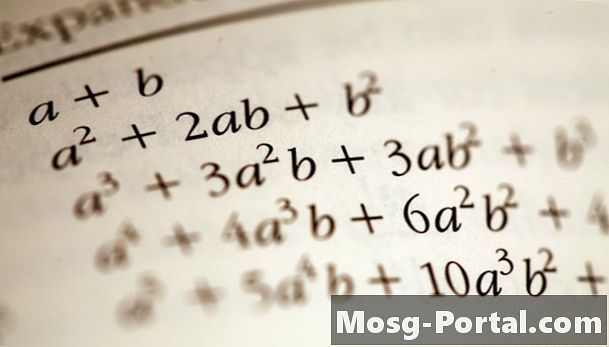
Contenu
- TL; DR (Trop long; n'a pas lu)
- Calcul du cube d'un binôme
- Qu'en est-il de la soustraction?
- Attention à la somme et à la différence des cubes
L'algèbre est pleine de motifs répétitifs que vous pouvez résoudre en calculant chaque fois. Mais étant donné que ces modèles sont si courants, il existe généralement une formule pour faciliter les calculs. Le cube d’un binôme en est un bon exemple: si vous deviez vous en sortir à chaque fois, vous passeriez beaucoup de temps à travailler au crayon et au papier. Mais une fois que vous connaissez la formule pour résoudre ce cube (et quelques astuces pratiques pour vous en souvenir), trouver votre réponse est aussi simple que de brancher les bons termes dans les bons emplacements variables.
TL; DR (Trop long; n'a pas lu)
La formule du cube d'un binôme (une + b) est:
(une + b)3 = une3 + 3_a_2b + 3_ab_2 + b3
Calcul du cube d'un binôme
Il n'y a pas besoin de paniquer quand vous voyez un problème comme (a + b)3 devant toi. Une fois que vous aurez décomposé ses éléments en composants familiers, vous commencerez à ressembler à des problèmes de mathématiques plus familiers que vous avez déjà connus.
Dans ce cas, il est utile de se rappeler que
(a + b)3
est le même que
(a + b) (a + b) (a + b), qui devrait paraître beaucoup plus familier.
Mais au lieu de faire le calcul à partir de zéro à chaque fois, vous pouvez utiliser le "raccourci" d’une formule qui représente la réponse que vous obtiendrez. Voici la formule pour le cube d'un binôme:
(a + b)3 = un3 + 3a2b + 3ab2 + b3
Pour utiliser la formule, identifiez les nombres (ou variables) qui occupent les emplacements pour "a" et "b" du côté gauche de l'équation, puis substituez ces mêmes nombres (ou variables) aux emplacements "a" et "b". sur le côté droit de la formule.
Exemple 1: Résoudre (x + 5)3
Comme vous pouvez le voir, X occupe l'emplacement "a" dans la partie gauche de votre formule et 5 occupe l'emplacement "b". En remplaçant X et 5 dans le côté droit de la formule vous donne:
X3 + 3x25 + 3x52 + 53
Un peu de simplification vous rapproche d'une réponse:
X3 + 3 (5) x2 + 3 (25) x + 125
Et enfin, une fois que vous avez simplifié autant que vous le pouvez:
X3 + 15x2 + 75x + 125
Qu'en est-il de la soustraction?
Vous n'avez pas besoin d'une formule différente pour résoudre un problème comme (y - 3)3. Si vous vous en souvenez y - 3 est le même que y + (-3), vous pouvez simplement réécrire le problème pour 3 et le résoudre en utilisant votre formule familière.
Exemple 2: Résoudre (y - 3)3
Comme cela a déjà été discuté, votre première étape consiste à réécrire le problème 3.
Ensuite, rappelez-vous votre formule pour le cube d'un binôme:
(a + b)3 = un3 + 3a2b + 3ab2 + b3
Dans votre problème, y occupe l'emplacement "a" du côté gauche de l'équation et -3 occupe l'emplacement "b". Substituez-les dans les emplacements appropriés du côté droit de l'équation, en prenant bien soin de mettre entre parenthèses votre nom pour préserver le signe négatif devant -3. Cela vous donne:
y3 + 3 ans2(-3) + 3y (-3)2 + (-3)3
Il est maintenant temps de simplifier. Encore une fois, faites très attention à ce signe négatif lorsque vous appliquez des exposants:
y3 + 3 (-3) y2 + 3 (9) y + (-27)
Un dernier tour de simplification vous donne votre réponse:
y3 - 9 ans2 + 27y - 27
Attention à la somme et à la différence des cubes
Portez toujours une attention particulière à la position des exposants dans votre problème. Si vous voyez un problème dans le formulaire (a + b)3, ou 3, alors la formule discutée ici est appropriée. Mais si votre problème ressemble à (une3 + b3) ou (une3 - b3), ce n’est pas le cube d’un binôme. C'est la somme des cubes (dans le premier cas) ou la différence de cubes (dans le second cas), auquel cas vous appliquez l'une des formules suivantes:
(une3 + b3) = (a + b) (a2 - ab + b2)
(une3 - b3) = (a - b) (a2 + ab + b2)