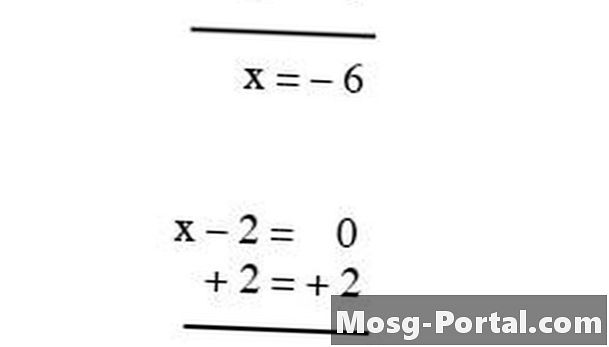
Contenu
La factorisation des équations est l’une des bases de l’algèbre. Vous pouvez trouver la réponse à une équation complexe beaucoup plus facilement en la divisant en deux équations simples. Bien que le processus puisse sembler difficile au début, il est en réalité assez simple. En gros, vous diviserez l’équation en deux unités qui, multipliées ensemble, créeront l’objet original. Vous pouvez factoriser et résoudre des équations en quelques étapes seulement.
Définissez votre équation sur 0. Supposons qu'une équation telle que x ^ 2 + 7x = --12 vous soit présentée. Vous ajouterez 12 aux deux côtés de l'équation pour la définir sur 0. Une fois que vous aurez fait cela, votre équation se présentera. comme ceci: x ^ 2 + 7x + 12 = 0.
Trouvez les facteurs. Dans ce cas, vous avez maintenant x ^ 2 + 7x + 12 = 0. Vous trouverez les facteurs de 12. Les facteurs de 12 comprennent 1, 2, 3, 4, 6 et 12.
Assurez-vous que vos facteurs totalisent la variable du milieu. Parmi tous les facteurs trouvés à l'étape 2, seuls 3 et 4 totalisent 7, la variable du milieu. S'assurer que les facteurs s'ajoutent à la variable centrale est la clé de la factorisation.
Factor vos variables inconnues. Puisque x est au carré, lorsque vous le factorisez, vous aurez un x. Voir la section suivante pour en savoir plus sur le traitement des variables inconnues.
Ecrivez votre nouvelle équation. Puisque 3 et 4 semblent avoir raison, écrivez votre équation sous la forme (x + 3) (x + 4) = 0.
Résoudre. Vous pouvez maintenant configurer votre équation pour résoudre x. Dans cette situation, vous auriez x + 3 = 0 et x + 4 = 0. Les deux vous montreraient que x = --3 et x = --4.
Vérifiez votre équation en remplaçant vos x par vos solutions: --3 ^ 2 + 7 (- 3) + 12 = 0 9 + (--21) + 12 = 0 21 + (--21) = 0
--4^2 + 7(--4) + 12 = 0 16 + (--28) + 12 = 0 28 + (--28) = 0
Définissez l'équation sur 0 et factorisez-la comme vous l'avez fait aux étapes 1 et 2 de la dernière section si votre équation a une valeur numérique négative. Par exemple, une équation telle que x ^ 2 + 4x - 12 = 0 peut vous être présentée.
Trouvez les facteurs dans x ^ 2 + 4x - 12 = 0. Pour cette équation, les facteurs sont 1, --1, 2, --2, 3, --3, 4, --4, 6, -. 6, --12 et 12 pour le nombre 12. Comme votre dernière variable est négative, ses facteurs seront positifs et négatifs. Dans cette situation, vos facteurs sont 6 et --2, car multipliés ensemble, ils ont un produit de -12, et une fois additionnés, leur produit est 4. Votre réponse ressemblera maintenant à (x + 6) ( x - 2) = 0.
Résous pour x comme tu l'as fait dans la dernière section; x sera égal à -6 et 2. Voir la figure 1.
Vérifiez votre équation en mettant vos solutions à la place de x. (--6) ^ 2 + 4 (- 6) - 12 = 0 36 + (--24) - 12 = 0 36 + (--36) = 0
2^2 + 4(2) -- 12 = 0 4 + 8 -- 12 = 0 12 -- 12 = 0